Received: November 2020
DOI 10.17677/fn20714807.2020.06.02
Fluorine Notes, 2020, 133, 3-4
QUANTUM-CHEMICAL CALCULATION OF ANTIVIRAL DEXAMETHASONE MEDICATION BY MNDO, AB INITIO AND DFT METHODS
V.A. Babkin1, D.S. Andreev1, Yu.A. Vashuta1, A.V. Kozhukhova1, V.S. Belousova2, E.S. Titova3,4, A.R. Titova4, A.I. Rakhimov3, A.K. Brel4, R.O. Boldyrev5, M.I. Artsis5, G.E. Zaikov5
1Volgograd State Technical University (Sebryakovsky br.), 403343 Volgograd Region, Mikhailovka, Michurina st., 21.
e-mail: babkin_v.a@mail.ru
2I.M. Sechenov 1st Moscow State Medical University, 119991, st. Trubetskaya, 8, bld. 2.
e-mail: desdemosha@mail.ru
3Volgograd State Technical University, 400005 Volgograd, Lenin av., 28.
e-mail: organic@vstu.ru
4Volgograd State Medical University, 400131 Pavshikh Bortsov sq., 1.
e-mail titova051@rambler.ru
5N. M. Emanuel Institute of Biochemical Physics RAS, 119334, Moscow, Kosygina st., 4.
e-mail: chembio@sky.chph.ras.ru
Abstract: For the first time, the calculation of the antiviral dexamethasone medication was performed using the classical quantum-chemical methods MNDO, DFT and AB INITIO. Its acidic strength is theoretically estimated (pKa = 12-14). It was found that this medication belongs to the class of weak acids (9 <pKa <14). It has been hypothesized that the effectiveness of dexamethasone is determined by its acidic strength.
Keywords: dexamethasone, acid strength, quantum-chemical calculation, AB INITIO method, DFT method, pKa is a universal indicator of acidity.
Introduction
A study carried out in Oxford proved that dexamethasone (8S,9R,10S,11S,13S,14S, 16R,17R)-9-fluoro-11,17-dihydroxy-17-(2-dihydro-xiacetyl)-10,13,16-trimethyl-6,7,8,11,12,14,15,-16-oxyhydrocyclopenta[a]phenanthrene-3-, (C22H29FO5) as an anti-inflammatory medication that reduces the risk of death of COVID-19 in those patients, who plugged to lung ventilator, by 35%, and among patients who received oxygen, by 20% [1]. For this reason, dexamethasone is currently being actively studied as a potential treatment for coronavirus infection COVID-19. Therefore, it is obvious that the problem of studying and increasing the effectiveness of this medication is very relevant. One of the ways to increase its effectiveness is to solve the issue of regulating its acidic strength and determining its maximum efficiency/selectivity of action in various biochemical reactions.
Therefore, the purpose of this report is a theoretical assessment of acidic strength of dexamethasone. To pursuing this objective, a quantum-chemical calculation of its optimal geometric and electronic structure (pKa) was carried out, as well as obtaining various quantum-chemical parameters characterizing this medication (Eo is the total energy of C22H29FO5 molecule, Eel - its total electron energy, qA - distribution of atomic electron density, and, in particular, qH+max - distribution of maximum atomic hydrogen charges). The results obtained can be used in other studies, for example, when studying the mechanisms of various reactions in which dexamethasone can participate.
Methodical part
For quantum-chemical calculation of studied dexamethasone [3] three methods were chosen: MNDO, AB INITIO/6-311G* and DFT-PBEO/6-311G**, the advantages and disadvantages of which are described in sufficient detail, for example, in monographs [4, 5]. The calculations were carried out within the molecular model in the gas phase using the program [6, 7, 8] similarly to [9-11]. The total charge of the molecular system of dexamethasone in all models is zero, since the calculation was performed in the ground state. Therefore, M = 1 (M - multiplicity), since M = 2S + 1, therefore, the total type is zero, since in the ground state all electrons are paired.
Calculation results
Optimized geometric and electronic structure of dexamethasone molecule is shown in Fig. 1 (AB INITIO method), in Fig. 2 (DFT method), and Fig. 3 (MNDO method). The quantum-chemical parameters (E0, Eel, qmaxH+) and pKa of studied compound are presented in Table 1. For model of dexamethasone obtained by AB INITIO method, the optimized bond lengths between carbon atoms in the ring are within the range 1.32-1.59 Å, for C-O- - within the range 1.19 -1.40 Å, for C-H- - within the range 1.07- 1.09 Å, for HO- - are equal 0.94 Å, and for FC- - are equal 1.39 Å.
Optimized values of bond angles (in degrees) are obtained, respectively, as follows: C(5)-C(6)-C(1)- 122, C(1)-C(2)-C(3)-123, C(10)-C(4)-C(3)-108, C(2)-C(3)-C(4)-123, C(14)-C(10)-C(4)-116, C(7)-C(3)-C(4)-116, C(9)-C(10)-C(4)-112, C(3)-C(4)-C(5)-111, C(10)-C(4)-C(5)-112, C(23)-C(4)-C(5)-105, C(4)-C(5)-C(6)-125, C(2)-C(1)-C(6)-115, C(2)-C(3)-C(7)-121, C(3)-C(7)-C(8)-109, C(10)-C(9)-C(8)-112, C(7)-C(8)-C(9)-111, C(14)-C(10)-C(9)-109, C(13)-C(14)-C(10)-113, O(22)-C(14)-C(10)-113, C(8)-C(9)-C(11)-111, C(10)-C(9)-C(11)-115, C(17)-C(12)-C(11)- 104, C(9)-C(11)-C(12)- 114, C(16)-C(17)-C(12)- 105, C(15)-C(11)-C(12)-104, C(18)-C(17)-C(12)- 111, O(26)-C(17)-C(12)- 111, C(11)-C(12)-C(13)- 108, C(17)-C(12)-C(13)- 109, C(37)-C(12)-C(13)- 109, C(12)-C(13)-C(14)- 115, C(9)-C(11)-C(15)- 118, C(11)-C(15)-C(16)- 104, C(15)-C(16)-C(17)- 106, C(20)-C(16)-C(17)- 114, C(16)-C(17)-C(18)- 112, O(26)-C(17)-C(18)- 107, C(17)-C(18)-C(19)- 123, O(21)-C(18)-C(19)- 118, C(15)-C(16)-C(20)- 114, C(17)-C(18)-O(21)- 120, C(13)-C(14)-O(22)- 108, C(3)-C(4)-C(23)- 109, C(10)-C(4)-C(23)- 111, C(14)-C(10)-F(24)- 106, C(18)-C(19)-O(25)- 111, C(16)-C(17)-O(26)-111, C(2)-C(1)-O(27)- 122, C(1)-C(2)-H(28)- 115, C(4)-C(5)-H(29)- 116, C(5)-C(6)-H(30)-122, C(1)-C(6)-H(30)- 117, C(3)-C(7)-H(31)- 110, C(3)-C(7)-H(32)- 110, C(7)-C(8)-H(33)- 110, C(7)-C(8)-H(34)- 109, C(8)-C(9)-H(35)- 107, C(10)-C(9)-H(35)- 105, C(9)-C(11)-H(36)- 105, C(11)-C(12)-C(37)- 113, C(17)-C(12)-C(37)- 113, C(12)-C(13)-H(38)- 110, C(12)-C(13)-H(39)- 110, C(13)-C(14)-H(40)- 110, C(11)-C(15)-H(41)- 113, C(11)-C(15)-H(42)- 111, C(15)-C(16)-H(43)-106, C(18)-C(19)-H(44)-112, C(18)-C(19)-H(45)-106, C(16)-C(20)-H(46)-111, C(16)-C(20)-H(47)-112, C(16)-C(20)-H(48)-110, C(14)-O(22)-H(49)-109, C(4)-C(23)-H(50)-113, C(4)-C(23)-H(51)-111, C(4)-C(23)-H(52)-109, C(19)-O(25)-H(53)-108, C(17)-O(26)-H(54)-109, C(12)-C(37)-H(55)-111, C(12)-C(37)-H(56)-112, C(12)-C(37)-H(57)-113. Atomic charges: C(1)- (+0.387), C(2)- (-0.137), C(3)- (-0.034), C(4)-(-0.319), C(5)- (+0.018), C(6)- (-0.159), C(7)- (-0.092), C(8)- (-0.129), C(9)- (-0.188), C(10)- (+0.30), C(11)- (-0.12), C(12)- (-0.428), C(13)- (-0.044), C(14)- (+0.203), C(15)- (-0.086), C(16)- (-0.245), C(17)- (+0.248), C(18)- (+0.283), C(19)- (+0.14), C(20)- (-0.146), O(21)- (-0.471), O(22)- (-0.492), C(23)- (-0.179), F(24)- (-0.427), O(25)- (-0.466), O(26)- (-0.514), O(27)- (-0.447), H(28)- (+0.099), H(29)- (+0.151), H(30)- (+0.111), H(31)- (+0.114), H(32)- (+0.113), H(33)- (+0.103), H(34)- (+0.126), H(35)- (+0.12), H(36)- (+0.107), C(37)-(-0.164), H(38)- (+0.124), H(39)- (+0.12), H(40)- (+0.112), H(41)- (+0.108), H(42)- (+0.132), H(43)- (+0.103), H(44)- (+0.114), H(45)- (+0.11), H(46)- (+0.107), H(47)- (+0.087), H(48)- (+0.088), H(49)- (+0.258), H(50)- (+0.097), H(51)- (+0.116), H(52)- (+0.122), H(53)- (+0.268), H(54) –(+0.276), H(55)- (+0.119), H(56)- (+0.093), H(57)- (+0.105) (see Fig.1).
For model of dexamethasone obtained by DFT method, the optimized bond lengths between carbon atoms in the ring are within the range of 1.33-1.59 Å, for C-O- - within the range of 1.22-1.41 Å, for C-H- - within the range of 1.08-1.10 Å, for HO- - within the range of 0.96-0.97 Å, and for FC – are equal 1.41 Å. C(5)-C(6)-C(1)- 122, C(1)-C(2)-C(3)-124, C(10)-C(4)-C(3)-107, C(2)-C(3)-C(4)-123, C(14)-C(10)-C(4)-116, C(7)-C(3)-C(4)-116, C(9)-C(10)-C(4)-112, C(3)-C(4)-C(5)-112, C(10)-C(4)-C(5)-111, C(23)-C(4)-C(5)-106, C(4)-C(5)-C(6)-124, C(2)-C(1)-C(6)-115, C(2)-C(3)-C(7)-121, C(3)-C(7)-C(8)-109, C(10)-C(9)-C(8)-112, C(7)-C(8)-C(9)-111, C(14)-C(10)-C(9)-110, C(13)-C(14)-C(10)-112, O(22)-C(14)-C(10)-112, C(8)-C(9)-C(11)-111, C(10)-C(9)-C(11)-115, C(17)-C(12)-C(11)-104, C(9)-C(11)-C(12)-114, C(16)-C(17)-C(12)-105, C(15)-C(11)-C(12)-104, C(18)-C(17)-C(12)-110, O(26)-C(17)-C(12)-111, C(11)-C(12)-C(13)-108, C(17)-C(12)-C(13)-108, C(37)-C(12)-C(13)-110, C(12)-C(13)-C(14)-115, C(9)-C(11)-C(15)-117, C(11)-C(15)-C(16)-105, C(15)-C(16)-C(17)-106, C(20)-C(16)-C(17)-114, C(16)-C(17)-C(18)-112, O(26)-C(17)-C(18)-107, C(17)-C(18)-C(19)-123, O(21)-C(18)-C(19)-118, C(15)-C(16)-C(20)-114, C(17)-C(18)-O(21)-119, C(13)-C(14)-O(22)-108, C(3)-C(4)-C(23)-110, C(10)-C(4)-C(23)-111, C(14)-C(10)-F(24)-105, C(18)-C(19)-O(25)-111, C(16)-C(17)-O(26)-112, C(2)-C(1)-O(27)-122, C(1)-C(2)-H(28)-116, C(4)-C(5)-H(29)-115, C(5)-C(6)-H(30)-122, C(1)-C(6)-H(30)-116, C(3)-C(7)-H(31)-110, C(3)-C(7)-H(32)- 110, C(7)-C(8)-H(33)- 110, C(7)-C(8)-H(34)-109, C(8)-C(9)-H(35)-107, C(10)-C(9)-H(35)-105, C(9)-C(11)-H(36)-105, C(11)-C(12)-C(37)-114, C(17)-C(12)-C(37)-113, C(12)-C(13)-H(38)- 110, C(12)-C(13)-H(39)- 110, C(13)-C(14)-H(40)- 110, C(11)-C(15)-H(41)-113, C(11)-C(15)-H(42)-111, C(15)-C(16)-H(43)-107, C(18)-C(19)-H(44)-112, C(18)-C(19)-H(45)-106, C(16)-C(20)-H(46)-111, C(16)-C(20)-H(47)-112, C(16)-C(20)-H(48)-110, C(14)-O(22)-H(49)-107, C(4)-C(23)-H(50)-113, C(4)-C(23)-H(51)-111, C(4)-C(23)-H(52)-109, C(19)-O(25)-H(53)-105, C(17)-O(26)-H(54)-106, C(12)-C(37)-H(55)-110, C(12)-C(37)-H(56)-112, C(12)-C(37)-H(57)-113. Atomic charges: C(1)- (+0.246), C(2)- (-0.102), C(3)- (+0.011), C(4)- (-0.36), C(5)- (+0.012), C(6)- (-0.133), C(7)- (-0.184), C(8)- (-0.186), C(9)- (-0.206), C(10)- (+0.20), C(11)- (-0.151), C(12)- (-0.423), C(13)-(-0.098), C(14)- (+0.079), C(15)- (-0.15), C(16)- (-0.264), C(17)- (+0.142), C(18)- (+0.195), C(19)- (+0.019), C(20)- (-0.255), O(21)- (-0.375), O(22)- (-0.393), C(23)- (-0.268), F(24)- (-0.322), O(25)- (-0.392), O(26)- (-0.40), O(27)- (-0.355), H(28)- (+0.101), H(29)- (+0.152), H(30)- (+0.114), H(31)- (+0.145), H(32)- (+0.139), H(33)- (+0.133), H(34)- (+0.156), H(35)- (+0.157), H(36)- (+0.138), C(37)- (-0.244), H(38)- (+0.156), H(39)- (+0.146), H(40)- (+0.142), H(41)- (+0.139), H(42)- +0.154), H(43)- (+0.137), H(44)- (+0.149), H(45)- (+0.144), H(46)- (+0.135), H(47)- (+0.123), H(48)- (+0.122), H(49)- (+0.248), H(50)-(+0.127), H(51)- (+0.143), H(52)- (+0.153), H(53)- (+0.250), H(54) –( +0.250), H(55)- (+0.145), H(56)- (+0.122), H(57)- (+0.132) (see Fig. 2).
For model of dexamethasone obtained by MNDO method, the optimized bond lengths between carbon atoms in the ring are within the range of 1.35-1.61 Å, for C-O- -within 1.23-1.40 Å, for С-Н- - within the range of 1.09-1.12 Å, for H-O- - are equal 0.95 Å, and for F-C- - are equal 1.36 Å.
Optimized values of bond angles (in degrees) are obtained, respectively, as follows: C(5)-C(6)-C(1)- 122, C(1)-C(2)-C(3)-124, C(2)-C(3)-C(4)-123, C(7)-C(3)-C(4)-117, C(3)-C(4)-C(5)-110, C(23)-C(4)-C(5)-104, C(4)-C(5)-C(6)-126, C(2)-C(1)-C(6)-115, C(2)-C(3)-C(7)-120, C(3)-C(7)-C(8)-112, C(7)-C(8)-C(9)-113, C(14)-C(10)-C(9)-107, C(8)-C(9)-C(10)-113, C(13)-C(14)-C(10)-114, C(11)-C(9)-C(10)-117, O(22)-C(14)-C(10)-113, C(8)-C(9)-C(11)-112, C(9)-C(11)-C(12)- 116, C(15)-C(11)-C(12)-106, C(11)-C(12)-C(13)-109, C(37)-C(12)-C(13)-109, C(12)-C(13)-C(14)-117, C(9)-C(11)-C(15)-118, C(11)-C(15)-C(16)-108, C(15)-C(16)-C(17)-107, C(20)-C(16)-C(17)-118, C(16)-C(17)-C(18)-112, O(26)-C(17)-C(18)-107, C(17)-C(18)-C(19)-123, O(21)-C(18)-C(19)-119, C(15)-C(16)-C(20)-113, C(17)-C(18)-O(21)-118, C(13)-C(14)-O(22)-110, C(3)-C(4)-C(23)-109, C(9)-C(10)-F(24)-111, C(14)-C(10)-F(24)-108, C(18)-C(19)-O(25)-114, C(16)-C(17)-O(26)-107, C(2)-C(1)-O(27)-122, C(1)-C(2)-H(28)-115, C(4)-C(5)-H(29)-116, C(5)-C(6)-H(30)-121, C(1)-C(6)-H(30)-117, C(3)-C(7)-H(31)-110, C(3)-C(7)-H(32)-111, C(7)-C(8)-H(33)-108, C(7)-C(8)-H(34)-109, C(8)-C(9)-H(35)-105, C(9)-C(11)-H(36)-103, C(11)-C(12)-C(37)-112, C(12)-C(13)-H(38)-109, C(12)-C(13)-H(39)-110, C(13)-C(14)-H(40)-108, C(11)-C(15)-H(41)-110, C(11)-C(15)-H(42)-112, C(15)-C(16)-H(43)-107, C(18)-C(19)-H(44)-110, C(18)-C(19)-H(45)-108, C(16)-C(20)-H(46)-113, C(16)-C(20)-H(47)-111, C(16)-C(20)-H(48)-110, C(14)-O(22)-H(49)-114, C(4)-C(23)-H(50)- 114, C(4)-C(23)-H(51)-112, C(4)-C(23)-H(52)-110, C(19)-O(25)-H(53)-113, C(17)-O(26)-H(54)-114, C(12)-C(37)-H(55)-112, C(12)-C(37)-H(56)-112, C(12)-C(37)-H(57)-113. Atomic charges: C(1)- (+0.286), C(2)- (-0.102), C(3)- (-0.077), C(4)- (-0.007), C(5)- (-0.033), C(6)- (-0.131), C(7)- (+0.027), C(8)- (-0.001), C(9)- (-0.039), C(10)- (+0.169), C(11)- (-0.018), C(12)- (-0.088), C(13)- (-0.015), C(14)- (+0.116), C(15)- (-0.001), C(16)- (-0.035), C(17)- (+0.115), C(18)- (+0.154), C(19)- (+0.146), C(20)- (+0.057), O(21)- (-0.275), O(22)- (-0.317), C(23)- (+0.047), F(24)- (-0.235), O(25)- (-0.304), O(26)- (-0.311), O(27)- (-0.286), H(28)- (+0.078), H(29)- (+0.076), H(30)- (+0.082), H(31)- (+0.015), H(32)- (+0.018), H(33)- (+0.011), H(34)- (+0.024), H(35)- (+0.016), H(36)- (+0.009), C(37)- (+0.039), H(38)- (+0.021), H(39)- (+0.028), H(40)- (+0.041), H(41)- (+0.012), H(42)- (+0.032), H(43)- (+0.01), H(44)- (-0.002), H(45)- (+0.051), H(46)- (+0.007), H(47)- (+0.008), H(48)- (-0.009), H(49)- (+0.195), H(50)- (-0.002), H(51)- (+0.007), H(52)- (+0.007), H(53)- (+0.187), H(54) –( +0.199), H(55)- (+0.009), H(56)- (+0.001), H(57)- (-0.009) (see Fig.3).
According to formula pKa = 49.04-134.61 qmaxH+ [10] - for AB INITIO/6-311G** method, (where qmaxH+ = +0, 276), pKa = 51.048-150.078 qmaxH+ [11] - for DFT-PBE0/6-311G** method (where qmaxH+ = +0, 25), and pKa = 42.11-147.18 qmaxH+ [12] - for MNDO method (where qmaxH+ = +0, 199) () were found that pKa = 12, 13, 14, respectively.
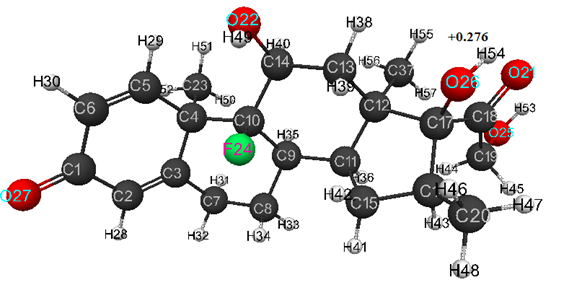
Figure 1. Geometric and electronic structure of dexamethasone molecule obtained by AB INITIO method.
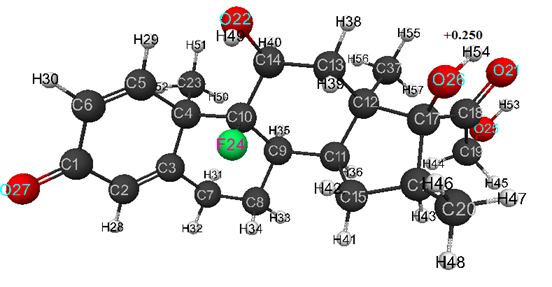
Figure 2. Geometric and electronic structure of dexamethasone molecule, obtained by DFT method.
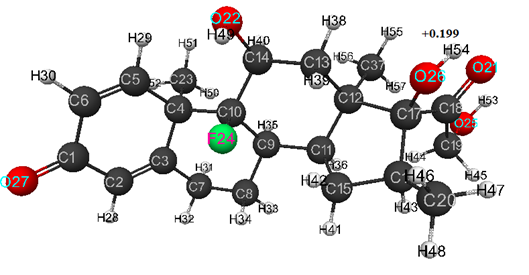
Figure 3. Geometric and electronic structure of dexamethasone molecule, obtained by MNDO method.
Table 1. Quantum-chemical parameters (E0, Eel, qmaxH+) and pKa of dexamethasone studied.
|
Preparation |
Method |
E0, kJ/mol |
Eel, kJ/mol |
qmaxH+ |
pKa |
|
Dexamethasone |
AB INITIO |
-3475589 |
-11311734 |
+0, 276 |
12 |
|
DFT |
-3492820 |
-11356356 |
+0, 25 |
14 |
|
|
MNDO |
-512487 |
-4309672 |
+0, 199 |
13 |
Thus, the optimized atomic-molecular structures of the studied medication (dexamethasone) were obtained by DFT, AB INITIO and MNDO methods. The quantum-chemical parameters (E0, Eel, qmaxH+) and distribution of atomic electron density (which is in full compliance with the law of charge conservation), etc., were calculated. It was proved that studied compound belongs to the class of weak acids (9 <pKa <14). It is obvious that proposed hypothesis – i.e. dependence of dexamethasone effectiveness on its acidic strength - requires experimental verification.
References
- Dexamethasone drug against coronavirus: expert commentary. [Electronic resource] - Access mode: https://www.kp.ru/daily/27144/4237679/ (12.08.2020)
- Quantum-chemical aspects of cationic polymerization of olefins, V.A. Babkin [et al.], 1996, Gilem Publishing House (Ufa), 188 pp. (in Russian).
- ru.wikipedia.org. Dexamethasone [electronic resource] (in Russian).
- Ermakov A.T. Quantum mechanics and quantum chemistry. - Yurayt Publishing House, 2016, 555 p. (in Russian).
- Cirelson V.G., Quantum Chemistry. Molecules, molecular systems and solids, Moscow, Publishing House «Binom», 2010, 496 p. (in Russian).
- General Atomic and Molecular Electronic Structure System, M.W. Schmidt [and others], J.Comput.Chem. 1993, 14, 1347-1363.
- MacMolPlt: A Graphical User Interface for GAMESS., B.M. Bode, M.S. Gordon, Journal of Molecular Graphics, 1998, 16, 133-138.
- Granovsky, A. A., Firefly version 8, 2013. http://classic.chem.msu.su/gran/firefly/index.html
- Connection of the universal acidity index of H-acid with the charge on Hydrogen atom (AB INITIO method). V. A. Babkin [and others], Oxidation Communications, 2002, 25(1), 21-47.
- Quantum-Chemical Calculation of Some Molecules of Triftoromethylstyroles by the DFT Method. V.А. Babkin [and others], Fluorine Notes, 2019, 123, 5-6
- Theoretical estimation of acidic strength of fluorine hydrogen - boron fluoride complexes. V. A. Babkin [and others], Intern. J. Polymeric. Mater, 2000, 47, 513-518.
ARTICLE INFO
Received 06 November 2020
Accepted 09 November 2020
Available online December 2020
Recommended for publication by by Prof. S.M. Igumnov
Fluorine Notes, 2020, 133, 3-4
