Received: February , 2014

Fluorine Notes, 2014, 93, 7-8

Theory Studies of Structural Properties, Energies and Natural Bond Orbital for a new fluorocarbonate compound

Shahriar Ghammamy ^a,*, NoorAhmad Qaitmas ^a, Amir Lashgari ^a

Department of Chemistry, Faculty of Science, Imam Khomeini International University, Qazvin, Iran
e-mail: ikiu2014@gmail.com, Tel: (+98) 281-8371378 Fax: (+98) 281-3780040

Abstract: In this theoretical study we used density functional theory to calculate the molecular structure of a fluoro carbonat compound that is COF₂. The molecular geometry, vibrational frequencies, energies and natural bond orbital (NBO) in the ground state are calculated by using the DFT (B3LYP) methods with 3-21G. Calculations were performed at the DFT level and split-valence plus polarization 3-21G basis sets were used. The T.S guesses were generated by the linear synchronous transit method, at the DFT implemented on Gaussian 98 program. Local minima were obtained by full geometrical optimization have all positive frequencies. This molecule has C_s symmetries and bent shape. The B3LYP calculated vibrational frequencies have been scaled by a single factor of 0.88 and 0.96 for all molecules to correct the well-known systematic 10–12% frequency over estimation. Infrared intensities (int) in Kilometer per mole of compound were performed at the same level on the respective fully optimized geometries.

Keywords: Theoretical studies, DFT, B3LYP, NBO, COF₂.

Introduction

In organic chemistry there are three important elements: carbon, oxygen and hydrogen. Every organic compound contains at least one atom of carbon. The distinction between organic and inorganic compounds is only a matter of convention, and there are several compounds that have been classified either way, such as: COCl₂, CSCl₂, CS(NH₂)₂, CO(NH₂)₂. There is a rich variety of carbon chemistry that does not fall within the realm of organic chemistry and is thus called inorganic carbon chemistry. There are many oxides of carbon (oxocarbons), of which the most common are carbon dioxide (CO₂) and carbon monoxide (CO). Fluorocarbons, sometimes referred to as perfluorocarbons or PFCs, are organofluorine compounds that contain only carbon and fluorine bonded together in strong carbon–fluorine bonds. Fluoroalkanes that contain only single bonds are more chemically and thermally stable than alkanes. However, fluorocarbons with double bonds (fluoroalkenes) and especially triple bonds (fluoroalkynes) are more reactive than their corresponding hydrocarbons. Fluoroalkanes can serve as oil-repellent/water-repellent fluoropolymers, solvents, liquid breathing research agents, and powerful greenhouse gases. Unsaturated fluorocarbons tend to be used as reactants. Fluorocarbon liquids are colorless. They have high density, up to over twice that of water, due to their high molecular weight. Low intermolecular forces give the liquids low viscosities when compared to liquids of similar boiling points. Also, low surface tension, heats of vaporization, and refractive indices are notable. They are not miscible with most organic solvents (e.g., ethanol, acetone, ethyl acetate and chloroform), but are miscible with some hydrocarbons (e.g., hexane in some cases). They have very low solubility in water, and water has a very low solubility in them (on the order of 10 ppm). The number of carbon atoms in a fluorocarbon molecule largely determines most physical properties. The greater the number of carbon atoms, the higher the boiling point, density, viscosity, surface tension, critical properties, vapor pressure and refractive index. Gas solubility decreases as carbon atoms increase, while melting point is determined by other factors as well and is thus not readily predicted. Many different data have been found about the structural properties of fluorocarbonate compound, but they are insufficient and opposing in somewhere. A primitive synthesized fluorocarbonate compound is COF₂, which used for structural chemistry studies and organic synthesis [1-7].

Theoretical calculations have been used for extraction of structural and electronically data of many compounds especially fluorocarbonate compound. In this research density functional theory methods were employed to determine the optimized structure of COF₂. There is not found any theoretical calculations for these type of compounds specially density function theory (DFT) calculation. The calculation was done by using the Gaussian 98 programs For DFT, Becke’s three-parameter exchange functional was used in combination with the Lee–Yang–Parr correlation functional (B3LYP) with 3-21G basis set [8-10]. Seppelt synthesized new fluorocarbonate compound and in this paper we investigated other properties of them.

Material and Methods

Computational methods

All computational are carried out using Gaussian 98 program which combines the exact Hartree-Fock exchange with Becke^,s and uses the Lee-Yang-Parr correlation function in order to include the most important correlation effects. The structure of the molecule was completely optimized without any symmetry in all the levels. The optimized structural parameters were used in the vibrational frequency calculations at the DFT levels to characterize all stationary points as minima. Infrared intensities (int) in Kilometer per mole of compound were performed at the same level on the respective fully optimized geometries. This compound and its data are in accordance with recent works on the formation of four coordinate intermediates.

Results

The fluorocarbonate compound, COF₂ was studied and geometry optimizations were performed at the DFT/ 3-21G level and are shown in Figure 1. The COF₂, in which C (1) is bonded to the O (2) atom, has linear C-O structure with bond length 1.19 Å. C(1) is bonded to the F(3) and (4) atom, has a linear C–F structure with bond length 1.35 Å has a bent O– C –F structure with a bond angle of 126. Selected bond distances are illustrated in Figure 1. Selected angles are reported in Table 1. The geometries of compound were optimized at B3LYP/ 3-21G levels. Density functional theory methods were employed to determine the optimized structure of COF₂. Initial calculations were performed at the DFT level and split- valence plus polarization 3-21G basis sets were used. Local minima were obtained by full geometrical optimization have all positive frequencies. All calculations were carried out using the computer program GAUSSIAN 98.

Both the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are the main orbitals that take part in chemical stability. The HOMO represents the ability to donate an electron, LUMO as an electron acceptor represents the ability to obtain an electron the HOMO and LUMO energy calculated by B3LYP at 3-21G method Figure 2. This electronic absorption corresponds to the transition from the ground to the first excited state and is mainly described by one electron excitation from the highest occupied molecular or orbital (LUMO).

Atomic charges and bond orders are significant parameters for our investigation. These quantities are derived from the NBO population analysis. The NBO method is preferred to Mulliken charges, because the former provides an orbital picture that is closer to the classical Lewis structure. The NBO analysis involving atomic charges, bond orders as well as hybridizations of selected bonds are calculated at B3LYP/ 3-21G level. The hybridization of this molecule is SP that confirmed by structural Table 2. Second order perturbation theory analysis of Fock matrix in NBO basis for COF₂ is shown in table 3. This molecule has C_s symmetries and bent shape.

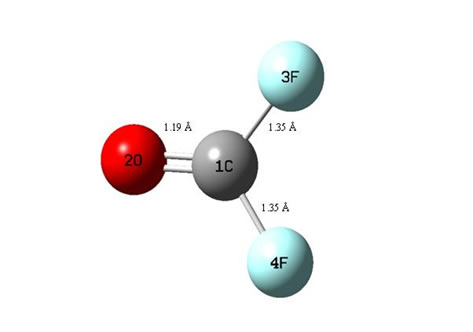
Figure 1. Optimized geometries of COF₂ at B3LYP/BS1 level of theory.

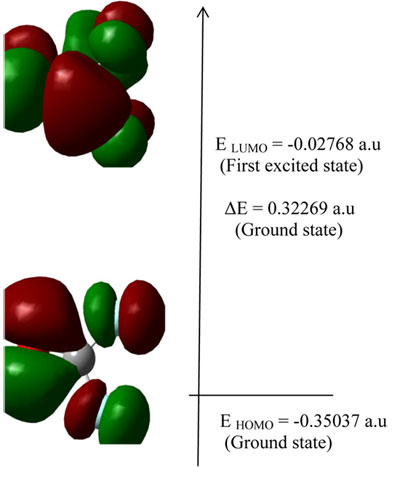
Figure 2. The atomic orbital compositions of the frontier molecular orbital for COF₂.

Table 1. Comparison of calculated bond angles (degrees) for the compound.

Compound	Θ
COF2	ΘO2C1F3=126
COF2	ΘO2CF4=126
COF2	ΘF3CF4=107.8

Table 2. The NBO Calculated Hybridizations for COF₂.

Bond	Atom	COF2
C-O(2)	C	S1P1.49
	O(2)	S1P1.61
C-O(2)	C	S1P1
	O(2)	S1P1
C-F(3)	C	S1P2.34
	F(3)	S1P3.26
C-F(4)	C	S1P2.34
	F(4)	S1P3.26
-	O(2)	S1P0.62
-	O(2)	S1P1
-	F(3)	S1P0.31
-	F(3)	S1P99.99
-	F(3)	S1P1

Table 3. Second order perturbation theory analysis of Fock matrix in NBO basis for COF₂. ^a E(2) means energy of hyper conjugative interaction (stabilization energy); ^b Energy difference between donor and acceptor i and j NBO orbital's; ^c F(i, j) is the Fock matrix element between i and j NBO orbital's.

Donor (i)	Type	ED/e	Acceptor (j)	Type	ED/e	E(2) a(KJ/mol)	E(j)-E(i) b(a.u)	F(i,j)c (a.u)
CO2 (2)	σ	1.99976	CO2 (2)	σ*	0.25720	2.61	0.37	0.030
CF3 (1)	σ	1.99049	CF4 (1)	σ*	0.16333	3.22	1.20	0.058
CF4 (1)	σ	1.99049	CF3 (1)	σ*	0.16333	3.22	1.20	0.058
O2 (1)	n	1.97365	CF3 (1)	σ*	0.16333	1.71	0.92	0.037
O2 (1)	n	1.97365	CF4 (1)	σ*	0.16333	1.71	0.92	0.037
F3 (1)	n	1.98849	CO2 (1)	σ*	0.04069	1.03	1.68	0.037
F4 (1)	n	1.98849	CO2 (1)	σ*	0.04069	1.03	1.68	0.037
CF3 (1)	σ*	0.16333	CO2 (1)	σ*	0.04069	1.46	0.37	0.065
CF4 (1)	σ*	0.16333	CO2 (1)	σ*	0.04069	1.46	0.37	0.065

Discussion

Calculations were performed using Gaussian 98 and Gauss View 5.0 molecular visualization program. The structures of the molecules were completely optimized without any symmetry in all the levels. The optimized structural parameters were used in the vibrational frequency calculations at the DFT levels to characterize all stationary points as minima. Geometry optimizations of DFT calculations were performed using Becke’s three-parameter hybrid functional with the Lee–Yang–Parr correlation function, a combination that gives rise to the well-known B3LYP method. The 3-21G basis set was used for all molecules B3LYP methods. Harmonic vibrational frequencies were computed using B3LYP methods with the 3-21G basis sets. The anharmonicity of the fundamental frequencies is most often taken into account by scaling the calculated harmonic frequencies, and this procedure has been found to work well since the overestimation of vibrational frequencies is fairly uniform. The B3LYP calculated vibrational frequencies have been scaled by a single factor of 0.88 and 0.96 for all molecules to correct the well-known systematic 10–12% frequency over estimation. Infrared intensities (int) in Kilometer per mole of compound were performed at the same level on the respective fully optimized geometries. This compound and their data are in accordance with recent works on the formation of four coordinate intermediates.

Acknowledgments We gratefully acknowledge the financial support from the Research Council of Imam Khomeini International University.

References

1. Lemal, D.M., 2004. Perspective on fluorocarbon chemistry. J. Org. Chem., 69: 1–11.
2. Lewandowski, G., E. Meissner, E. Milchert, 2006. Special applications of fluorinated organic compounds. J. Hazard. Mater, 136: 385–91.
3. O'Hagan, D., 2008. Understanding organofluorine chemistry. An introduction to the C–F bond. Chem. Soc. Rev., 37: 308–19.
4. Kiplinger J.L., Richmond TG, Osterberg CE (1994). "Activation of Carbon-Fluorine Bonds by Metal Complexes". Chem. Rev. 94 (2): 373–431.
5. Murphy C.D., C. Schaffrath, D., 2003. O'Hagan: Fluorinated natural products: the biosynthesis of fluoroacetate and 4-fluorothreonine in Streptomyces cattleya. Chemosphere, 52:455-61.
6. Steenland, K., T. Fletcher, D.A. Savitz, 2010. Epidemiologic Evidence on the Health Effects of Perfluorooctanoic Acid (PFOA) . Environmental Health Perspectives, 118: 1100–8.
7. Berthelot, M., 1891. Action de la chaleur sur l'oxyde de carbone. Annales de Chimie et de Physique, 6: 126–132.
8. Ando, Sh., 2006. DFT Calculations on Refractive Index Dispersion of Fluoro-compounds in the DUV-UV-Visible Region. Journal of Photopolymer Science and Technology, 19: 351-360.
9. Audi, G., 2003. The Nubase Evaluation of Nuclear and Decay Properties. Nuclear Physics,729: 3–128.
10. Becke, A.D., 1993. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys., 98: 5648-5652.

Recommended for publication by Prof. S.M. Igoumnov

Fluorine Notes, 2014, 93, 7-8