Back to volume # 3(82) , May - June 2012

Received: November, 2011

Fluorine Notes, 2012, 82, 5-6

Determination of the reaction rate constants of the synthesis of perfluoroethylisopropylketone in a flow conic reactor

I.M. Fenichev, Y.I. Babenko, T.A. Bispen, D.D. Moldavskiy, V.I. Manuylova

FCUE Russian Scientific Center "Applied Chemistry", 193232, Russia, St. Petersburg, Krilenko ave. 26A
e-mail: htf1352501@rambler.ru

Abstract:The method of determination of the reaction rate constants of the synthesis of perfluoroethylisopropylketone by the interaction between hexafluoropropene oxide or fluoroanhydride of perfluoropropionic acid and hexafluoropropene in a flow conic reactor. The rate constants of both gas reactions have been found.

Keywords: Perfluoroethylisopropylketone, a reaction rate constant, a conic reactor, an intermediate complex, cesium perfluoropropionate.

Searching for the rational methods of the synthesis of perfluoroethylisopropylketone, C₂F₅-C(O)-CF(CF₃)₂, (the ketone), we found that it can be obtained by the reaction between hexafluoropropene (hereinafter propene) and fluoroanhydride of perfluoropropionic acid (hereinafter fluoroanhydride) or the reaction between hexafluoropropene and hexafluoropropene oxide (hereinafter oxide) in the presence of catalysts KF or CsF:

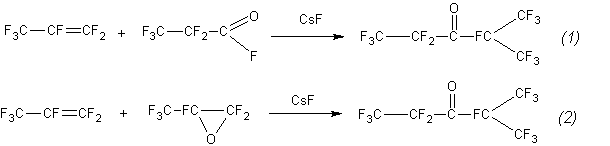
Both processes are exchangeable and proceed in the same conditions (catalyst, temperature, contact time, the yield of ketone, the composition and ratio of impurities).This case is a very rare in chemical practice. To investigate this phenomenon, we determined the rate constants of both reactions and suggested the mechanism of the interaction.

In the case of proceeding an irreversible bimolecular reaction in the gas phase in a confined space with conservation of the number of moles according to the scheme:

А + В → С + D,(3)

the determination of the reaction rate constant is not difficult since the corresponding system of kinetic equations is integrated and the specified constant can be found, for example, using the conversion of the starting materials [1].
In a tubular flow reactor the system of the kinetic equations retains the form if instead of reaction time t the term "residence time" which is given by the equation t = x/u (x - a current coordinate, u - a linear velocity of the gas) is used.

However, if the gas reaction, as in our case, proceeds in a confirmed space with a decreasing in the number of moles according to the scheme (4)

A + B → C, (4)

A simple kinetic model is not applicable because the molar concentrations of individual substances vary not only due to the chemical interaction but also because of the decreasing in the density of the mixture during the reaction which complicates the processing of experimental data. In this case it is possible to determine the rate constant only by the initial sections of kinetic curves when the density of the mixture is close to the original but the information about the nature of the process at high conversions is lost.

In this paper it has been developed a relatively simple way to eliminate this difficulty by using the appropriate equipment.

Method of determining of a rate constant of a reaction proceeding with a decreasing in a specific volume

We assume that the gas reaction (4) is carried out in a closed space, where the reaction volume simultaneously decreases with the decrease of the specific volume. In this case the system of kinetic equations can be written as follows:

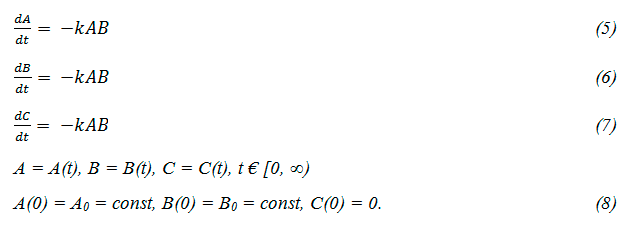
Here A, B, C - molar concentrations of the substances, t - time, k - reaction rate constant. In the process we have investigated the initial concentration of the initial substances are the same (A₀ = B₀). It is obvious that for any values of t we have A (t) = B (t). Therefore, instead of (5) it can be written:

Integrating the equation (9), we find

Combining equations (5) and (7) and integrating, we obtain

Equation (12) follows from equations(10) and (11)

In practice, the kinetic constant is convenient to define by the conversion of the initial substances ξ (in our case ξ₁ = ξ₂):

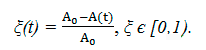
From (10) we find

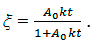
The basic formula for determining of the kinetic constant follows the the above calculations:

In practice it is too difficult to create a device that automatically reduces the volume during the process of the reaction. However, this difficulty is easily overcome if the process is carried out in a flow conic reactor which inlet cross- section is approximately twice as much output one. It is assumed that the value of conversion is close to 1. In the expression (13) by the value t we should mean a residence time of an elementary volume moving with the flow t = l / u, where l - length of the reactor channel.

About the hydrodynamics of the process

If the process proceeds in a flow reactor with a decrease in a specific volume, a loss of stability of a linear flow at Reynolds numbers much lower than the usual Re ≈ 2200 is possible. This results to the initiation of circulating currents and a simple calculation formula (13) becomes non-applicable. This question is theoretically investigated in [2]. The criterion of a loss of stability of a linear flow is given by:

Here, ρ - density, r - radius of a flow canal, v - kinematic viscosity of the medium.

In this form, this criterion is not directly connected with the Reynolds number, but depends on (mostly) on the relative change in density of the mixture Δp/p₀at a distance, having the order of the length of the reactor

Combining (14) and (15) and taking into account that Re = 2ur / v we obtain

The constant is not defined since the equation (15) is approximate, but it is obvious that its value has the previous order.

If the canal has the shape of a convergent cone, the flow is more stable than in a linear tube [3]. Thus, there is a "compensation effect" and the criterion value exceeds 5.76.

As in the process we studied the reactor contained the bulk catalyst we haver ≈ 10^-3. The criterion value of 5.76 is not reached in such a narrow canal. Therefore, circulating currents do not occur. However, if the filling was absent, a "smooth" flow behavior could not be realized, especially in a large industrial reactor. Therefore, the conic reactor can be used not only to determine the rate constants, but also to stabilize the flow in a flow reactor. The reactor design has been patented by the authors in Russia [4].

Experimental part

A liquid mixture of propene and propene oxide or propene and fluoroanhydride in the molar ratio of 1,02 ÷1,05: 1 is fed with a certain speed to the evaporator, which is a tube made of stainless steel, length of 300 mm,diameter of 28 mm, heated to the temperature of a starting zone of the reactor, and then is fed directly to the reactor. The reactor was welded from three coaxial tubes of stainless steel, length of 235 mm each and the inner diameters of 28, 23 and 17 mm respectively. The reactor is equipped with three pockets for thermocouples, control valves, pressure gauge, two controlled heating zones - 250 and 450 mm respectively. The reactor was filled with coal BAU-2 containing 20 wt% of CsF. The reactor pressure was maintained at 0.22 - 0.25 MPa (at this pressure by-product formation is minimized). The reaction products were collected in a trap of stainless steel cooled with liquid nitrogen. The reaction products were weighed and analyzed by GLC ("Kristall 2000M", column length of 2 m, silochrom +20% В О±, О±, О± - trisbetacianoethoxiacetophenon, thermal conductivity detector, He as a carrier gas).

The same reactor was used to study the isomerization of propene oxide to the anhydride.

Experimental data and the calculated rate constant

In the following tables Q is a total flow of a mixture at the inlet to the reactor, t - holding time. The calculation of the rate constant of reactions is carried out by the formula(13).

Table 1. The reaction of hexafluoropropene and hexafluoropropene oxide

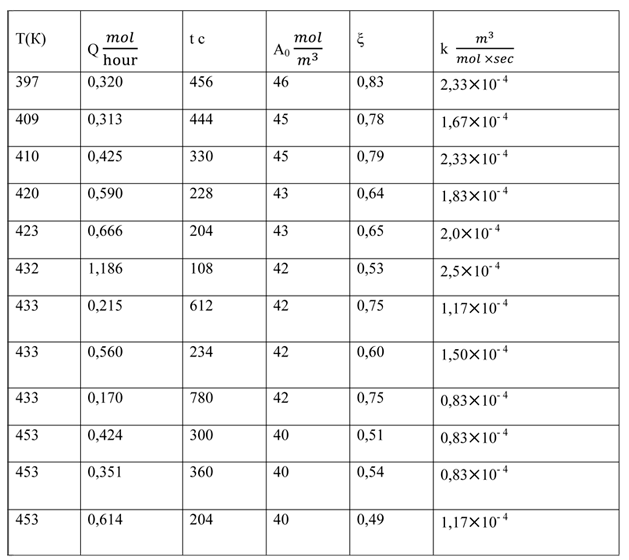
Table 2. The reaction of hexafluoropropene and anhydride

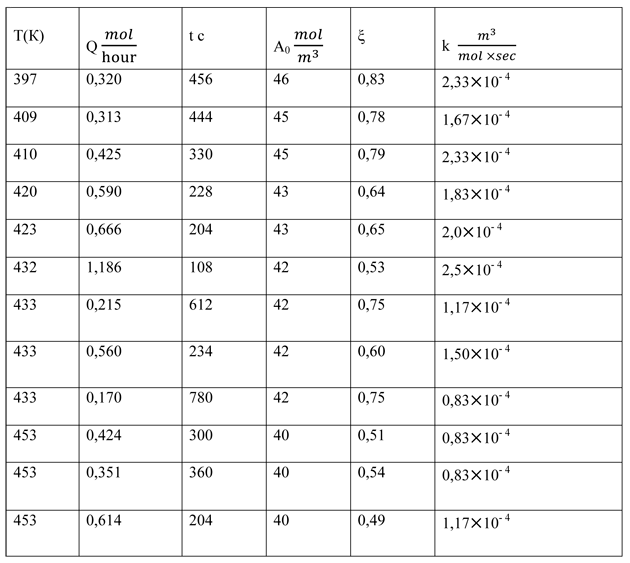
Despite the considerable scatter of the numerical values of the reaction rate constant, an inverse dependence of the gross reaction from the temperature is traced. This means that the reaction proceeds through an intermediate complex (cesium perfluoropropionate), which then reacts with the second component - propene [5]. Such processes are common [6]. Thus, the formal scheme (4) makes it impossible to find the value of k in the form k = k₀ exp (-E/RT).

We also obtained the individual data for the rate constants at different pressures in the range 1÷4,5*10⁵ Pa. In this case there is an inverse dependence of reaction rate on the pressure, which also indicates the formation of an intermediate complex.

The obtained information in spite of the limitations allowed to carry out the design and the creation of an industrial reactor for the ketone synthesis at a pilot plant FSUE RSC "Applied Chemistry".

We should note one feature of the results. Within the scatter of the obtained numerical values of the constants they are close for both studied reactions. The similarity of the rate constants of reactions (1) and (2), as well as the inverse dependence of the constant on the temperature indicates the following mechanism of the interaction where the first fast stage of the process is the formation of cesium perfluoropropionate [7,8]:

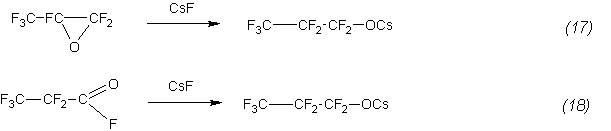
Then propionate reacts with a propene to form a ketone:

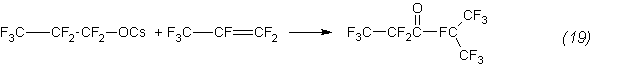
Additional confirmation of this is, in particular, the isomerization of an oxide to the anhydride, quantitatively proceeding even at 85°C:

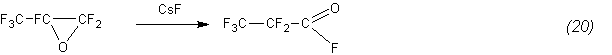
Conclusions

1. The method of the determination of the rate constant of the gross reactions for the synthesis of the perfluoroethylisopropylketone in a flow cone reactor is suggested.

2. According to this method the rate constants of two gas reactions have been found.

3. Similar values of the rate constants of both reactions support the hypothesis that the reactions proceed through the same intermediate complex, the formation rate of which is substantially greater than the decay rate.

References

E.T. Denisov. Kinetics of homogeneous chemical reactions. M. "High School", 1978., 368.
Y.I. Babenko, About the occurrence of turbulent flow regime in the presence of a chemical reaction. Inzhenerno-Fizicheskii Zhurnal (IFZh), 1986. Vol.50. N 2. Dep. in VINITI 29.08.85, Reg. N 6424-85 Dep.
N.E. Kochin, I.A. Kibel, N.V. Rose. Theoretical Hydromechanics. Part 2 .M., GIFML, 1963.
Pat. The Russian Federation. N 107073 from 10.08.2011.
R. D. Smith, F. S. Fawcett, D. D. Coffman, J. Amer, Chem, Soc., 84, 4285 (1962)
R. Schmid, V.N. Sapunov .В Informal kinetics. In search of the mechanisms of chemical reactions: Trans. from English .-M.: Mir, 1985. - 264, Ill.
R. D. Chambers e. a. J. Chem. Soc., C, 1968, 2221.
W.В Brunsgill e. a. J. Chem. Soc. Chem. Comm., 1970, 1444.