Fluorine Notes, 2010, 72, 3-4
ELECTROCHEMICAL FLUORINATION OF METHYL 3-METHOXYPROPIONATE
N. Lebedev, V. Berenblit,
Federal State Unitary Enterprise S.Y. Lebedev Research Institute for synthetic rubber (FSUE NIISK)
Gapsalskaya ave 1, St.-Petersburg, 198035, Russia
Abstract: Electrochemical fluorination (ECF) of methyl 3-methoxyporionate was studied. A formal kinetic analysis of the ECF multistage process was conducted, which confirmed experimentally by ECF of methyl 3-methoxyporionate and some others oxygen-containing compounds.
Keywords: ,Electrochemical fluorination (ECF), Methyl 3-methoxypropionate, Tafel equation, current yield
Studies regarding electrochemical fluorination (ECF) of organic compounds in the medium of anhydrous hydrogen fluoride at nickel anodes in electrolyzers of Saimons type had been started in the FSUE NIISK initiated by I. M. Dolgopolsky more than 50 years ago, in particular, for the purpose of synthesizing perfluoro-3-methoxipropionylfluoride [1]. That works even before Japaneese publications [2] had proved, that at electrochemical fluorination of esters the yield of perfluoroacylfluorides virtually had not yielded to the monitored one at fluorination of acylhalogenides.
The methyl 3-methoxypropionate ECF technology was developed in the Institute, after that the experimental-industrial set was created at Pilot Plant of VNIISK and in 1967 a process of continuous electrolysis in electrolyzers of box type was mastered. The duration of continuous process at stationary concentration of electrolyte supported by continuous feed of initial product into electrolyzer at current density of up to 3 A/dm2 had reached 2000 hours [3-6].
With the help of Gas Liquid Chromatography (GLC), NMR 19F (1H) spectroscopy the composition, structure were defined and the yields of practically all electrolysis products were calculated, the material balance of that electrolysis could be described by the scheme:

The ECF process of methyl 3-methoxypropionate in anhydrous hydrogen fluoride is accompanied by ester's hydrofluorolysis, that's why in products as opposed to elemental fluorine fluorination the perfluorinated ester is absent [6, 7].
It is obvious, that the process of replacing protons for fluorine at ECF of methyl 3-methoxypropionate has got many stages and at the last stage mainly perfluorinated products are being deleted out of electrolyte in gaseous phase. The yield of monohydroperfluoroderivatives doesn't exceed 10% mole.
The destruction by CH3O-CH2- bond leads to forming of perfluoropropionylfluoride, two isomeric tetrafluoropropionylfluorides and carbonyldifluoride, while at destruction by CH3-OCH2- bond difluoromalonyldifluoride and fluormethanes are formed.
The fluorination of acylfluoride group is accompanied by cyclization with forming of five and six-membered cycloethers [7]. In present case the formation of perfluorodioxane-1,3 and perfluorodioxolane-1,3 was observed. Exhaustive fluorination of acylfluoride group results in forming of perfluoromethylpropyl ether, while at destruction by C-C bond perfluoromethylethyl and three different pentafluoromethylethyl ethers are formed as well as trifluoroacetylfluoride. It is formed also due to destruction of medium C-C bond, which the formation of three different polyfluorodimethyl ethers proves.
During the ECF we often observe the isomerization leading to branching of carbon skeleton [8] that is the perfluoro-2-methoxypropionyl fluoride and perfluoromethoxyacetyl fluoride were found in ECF products.
The process of ECF passes with high overpotential without isolating of elemental fluorine, for which the meaning "A" in Tafel equation reaches 4 V [9]. This process is rather specific in regards to the material of anode, which is limited by nickel and carbon. Nickel in the process of fluorination is being covered with nickel fluoride, which adsorbs radical fluorine [10], while for the carbon the compounds of introduction are typical.
High overpotential shows low meaning of exchange current and slowness of fluorine-ion discharge electrochemical stage. The meanings of logarithmic coefficient in this equation at carbon and nickel [12-14] anodes adsorbing fluorine-radical at electrolysis in the medium of anhydrous hydrogen fluoride exceed more than twice the meanings discovered for platinum [14] which doesn't interact with fluorine. Taking into account rather low energy of bond in F2 molecule we should suppose, that interactions of adsorbed fluorine radical with organic substrate were the decelerated stages of the electrochemical process. As the organic substrate undergoes virtually exhaustive fluorination before it is deleted from electrolyzer, electrochemical fluorination is a multistage electrode process with few subsequent fluorination stages parallel to electrochemical process of discharge of ion fluorine and adsorption of radical fluorine at nickel fluoride:
![]()
At constant anode potential, which controls constant concentration of adsorbed fluorine radicals
at anode's surface and at constant concentration of protoned cation complexes and ion fluorine
in electrolyte the process of fluorination of organic compound can be displayed using the
following scheme with rate constants of every stage ki:
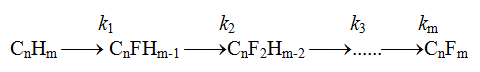
From the ideas of formal kinetics for the rate of first stage of fluorination described in electrical digits in the form of partial density of the current of first stage i1, we can record:

At steady feed of initial substrate with rate Δ[CnHm]/Δt = α<<[CnHm] the total derivative of concentration is equal to:
![]()
To solve the differential equation having changed the variable [CnHm] = х*ехр(-k1t) for the total derivative we'll record:
![]()
or:
![]()
thus:
![]()
Integrating we'll obtain:

or:

As under the boundary conditions: at t = 0;
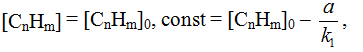
then

and partial density of current of first stage is equal to:
![]()
For the second stage we should record in partial derivatives:
![]()
As the concentration of first intermediate increases due to its appearance at first stage and decreases due to spending at second stage, its total derivative will be made of partial derivatives by 1 and second stages and equal to difference of partial densities of current of that stages:

Solving that equation under boundary conditions at t=0, [CnFHm-1] = 0,
and also with the replacement of the variable
[CnFHm-1]=x*exp(-k2t),
we will get:

And partial density of current is equal:
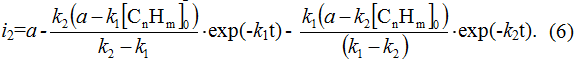
Analogously the equations for following stages of fluorination are being solved, in particular for the third stage:
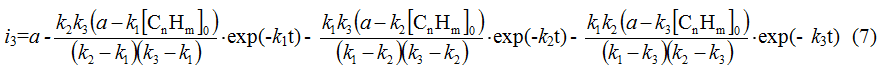
Accordingly the partial density of current of the last stage of process or the rate of forming of the end product will be expressed by the equation:

Only delayed stages of process, for which ky >> kx will influence the electrolysis
products isolation rate controlled apparently by slowness of desorption of polyfluorinated
compounds from the electrode surface. Then constants ky, included into fractional
products will diminish, and exponential members with constants, which differ dramatically
from the constant of a delayed stage can be ignored.
Then the equation (8) is being dramatically
simplified:
![]()
And it is becoming analogous to equation (3) for partial density of the first stage current. In this case the rate of last stage and, therefore the yield by the end product current will monotonically increase in time (Pic. 8), asymptomatically getting closer to the meaning

In the absence of feeding of initial compound during electrolysis, when the concentration of initial substrate decreases as it is consumed during fluorination, e.g. at α=0, the equation (9) obtains the form:
im = [CnHm]0 exp(-kxt).
At t = 0, in accordance with boundary conditions im = 0, at t → ∞ the exponent with negative indicator converges to zero and, therefore, im→ 0. Under real conditions it occurs at the end moment of time, when electrolyte is up and concentrations of fluorinated substrate and intermediates are approaching zero. In accordance with the Rolle's theorem under end meanings of multistage process rate the partial density of current of the last stage must have maximum at some meaning of τ.
The yield by current of multistage process of electrochemical fluorination with discharge of z electrons onto fluorine ion discharge and adsorption of fluorine radical is equal to:
A = zFd[CnFm]/dQ, where Q - the quantity of electricity consumed.
Current intensity of electrolysis J is equal to dQ/dt and, therefore, at constant current intensity of electrolysis the yield by current is equal to:
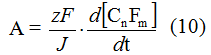
It is obvious, that the derivative of concentration of end product by time is a rate of forming of this product, e.g. the rate of last stage of electrolysis process. The yield by current is usually expressed in relation of the quantity of electricity consumed by present end product to the total quantity of consumed electricity (%). In case of individual product forming when the quantity of consumed Faradayies is known, that meaning can be calculated easily. However, at electrochemical fluorination of methyl 3-methoxypropionate, when due to variety of accompanying processes a range of products is formed, the yield by current is difficult to calculate and it is defined in grams per Ampere-hour.
In accordance with analysis conducted at absence of feeding in the initial methyl 3-methoxypropionate, experimental plot of current output in g/(A*h) is nearly symmetrical curve with a maximum (Pic. 1).

Picture 1. The Dependency Of Yield By Current On Time At One Time Feeding Of Substrate Into Electrolyzer.
At long-duration continuous electrolysis with feeding in of initial substrate into electrolyzer to support stationary concentration of electrolyte, the yield by current will correspond to equation:
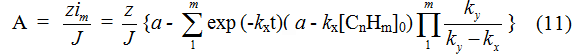
At α = k1[CnHm]0, when the feeding in of initial substrate into electrolyzer is equal to its consumption at first stage and its concentration doesn't change during the process, the equation for yield by current can be recorded as follows:
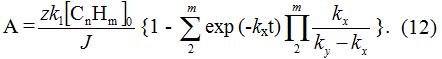
At t= 0, in accordance with boundary conditions A = 0; at τ → ∞ ,
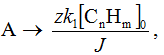 analogously to what is shown at Pic. 2 and confirmed by experimental dependency of yield
by current on time shown at Pic.3.
analogously to what is shown at Pic. 2 and confirmed by experimental dependency of yield
by current on time shown at Pic.3.
As the meaning k1 can't be strictly defined due to variety of reactions of destruction, cyclyzation of isomerization and etc., probably preceding the fluorination itself the meaning of feeding of the initial compound "α" is bound to be calculated using the electricity consumption for fluorination at electrolysis with one-time charge. Usually, such calculated meaning appears to be a little lower than the meaning k1[CnHm]0, as during such electrolysis a moment comes, when the initial substrate is already absent in electrolyte, and the current consumption for the fluorination of intermediates is going on and it (the meaning) is bound to be defined experimentally.

Pic. 2. The Dependency Of Yield By Current On Time At Constant Concentration Of Substrate In the ECF Process.
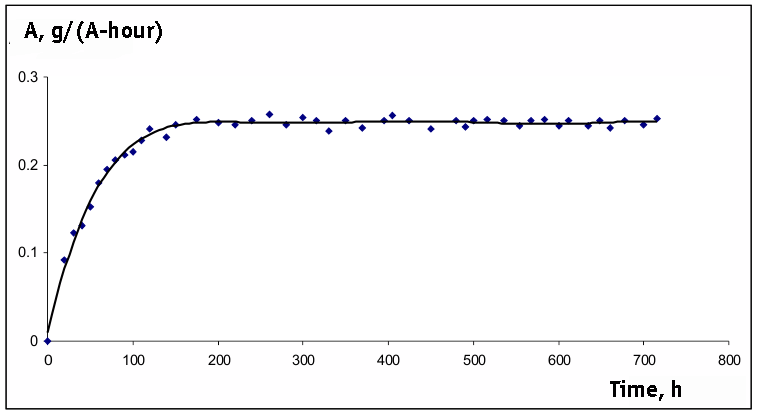
Pic. 3. Experimental Dependency of Yield By Current On Time At Constant Concentration Of Methyl
3-Methoxypropionate In The Process Of ECF
(U = 5 V).
In accordance with mathematical analysis at a α<k1[CnHm]0 the yield by current goes through the point of maximum under the real conditions decreasing in time due to electrolyte exhausting (Pic. 1). The attempts to correct the composition of electrolyte by the one-time adding of the initial product unexpectedly resulted in sharp descrease of the yield by current (Pic. 4).

Pic. 4. Experimental Dependency of Yield By Current on Time Period
At Periodical Correction of Electrolyte In The ECF of Methyl 3-Methoxypropionate.
The analysis of equation (12) proves, that during the alteration of concentration of [CnHm]0+Δ[CnHm] in case, if the first stage is slowed, then due to increase in partial current density of that stage, when the total current density is fixed by the current strength of electrolysis, their corresponding redistribution according to the following stages will be going as a result of which the yield by current must sharply decrease (Pic. 5), that is confirmed by the experimental data (Pic. 4).

Pic. 5. The Dependency Of Yield By Current On Time Period At One-Time Correction Of Concentration Of Substrate In The ECF Process.
Such a sharp decrease of the yield by current of end products at one-time correction leads to the decreasing of average yield by current of electrolysis and, therefore, the productivity of electrolyzer, and as well to rather significant scattering of meanings defined. Such scattering is probably connected to the periodicity of feeding of the starting product into electrolyzer at long term ongoing process and it disappeares at its ongoing feeding by controlled volume pump.
The exceeding of feeding of initial product also resulted in the lowering of yield by current due to accumulating of gum-like high-molecular products in the electrolyte, but it was a subject of a special consideration.
Thus, the conducted formal kinetic analysis of the multistage process of electrochemical fluorination is rather convincingly confirmed by experiments at electrochemical fluorination of methyl 3-methoxypropionate and some other oxygen containing compounds and probably it might be used at organization of ongoing electrolysis of other compounds.
References
[2] Nagase S., Kojama R. // Bull. Chem. Soc. Japan, 1961. V. 34. N 10. P.1460.
[3] Berenblit V.V., Byzov B.A., Grachev V.I. i dr.//ZhPKh. 1975. T. 58. № 3. s. 709.
[4] Berenblit V.V., Sass V.P., Senyushov L.N. i dr.//ZhOrKh. 1976. T. 12. № 4. s. 767.
[5] Berenblit V.V., Nikitin V.A., Sass V.P. i dr.//ZhOrKh. 1979. T. 15, № 2, s. 284.
[6] Patent JP 2002308828, 2002.Method for Producing Fluorine-Containing Compound.
[7] Patent US 6482979, 2002. Perfluorinated Acid Fluorides and Preparation Thereof.
[8] Patent US 2644823, 1953. Cyclical Ethers of Fluorocarbons.
[9] Hoffmann P.W., Simmons T.C., Beck R.B. et al.//J. Am. Chem. Soc. 1957. V. 79. P. 3424.
[10] Watanabe N. // Chem. and Chem. Ind. Japan («Kagaku to koge») 1965. V. 18. N 6. P. 825.
[11] Watanabe N., Chang B., Takashima M. / Report on V The Internat. Fluor. Chem.
Symp. Moscow, 1969.
[12] N.Hackerman, E.S.Snavely, L.D.Fiel // Electrochem. Acta. 1967. V. 12. N 5. P. 535.
[13] G.I.Kaurova, L.M.Grubina, TS.A.Adzhemyan// Elektrohim. 1969. V. 3. N 10. P. 1222.
[14] N.Watanabe, B.Chang, Denki Kagaku. 1969. V. 37. P. 198.
Fluorine Notes, 2010, 72, 3-4
